Knowledge Graph Reasoning and Completion
Knowledge Graph is a data structure that stores structured information, in which the associations between objects are stored in the form of triplets. For example, a geographical knowledge graph may include: (Beijing, Is_capital, China), which indicates that the capital of China is Beijing.

(caption: By representing entities as nodes and triplets as directed edges, a knowledge graph can be represented as a graph; picture source network)
The current knowledge graphs include both domain knowledge graphs limited to specific fields, such as medical knowledge graphs, geographical knowledge graphs, etc., and general knowledge graphs extracted from the network Wikipedia. The latter contains more objects and more complex relationships. The more well-known ones include: YAGO includes facts about people, cities, countries, organizations and movies; WikiData, with the extensive information of Wikipedia, has more than 100 million entities belonging to different categories.
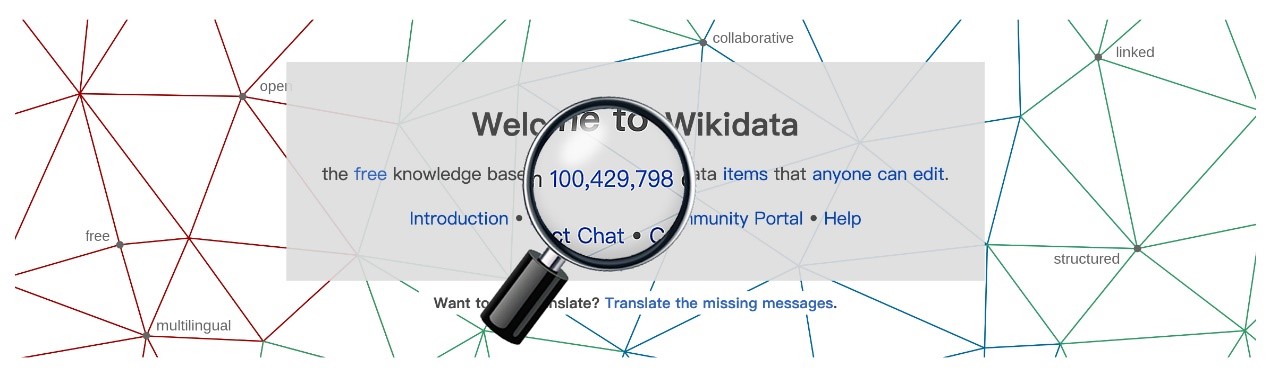
(caption: WikiData has information about more than 100 million objects, picture source: www.wikidata.org)
Because of its structured storage, an important application of knowledge graphs is to perform automatic reasoning on knowledge. By querying the stored information, the knowledge graph can start from a certain entity and find the answer along a specific relationship (predicate). Such technology can be used in question answering systems, search engines, expert systems, etc., to provide domain, common sense and encyclopedia knowledge for various tasks.
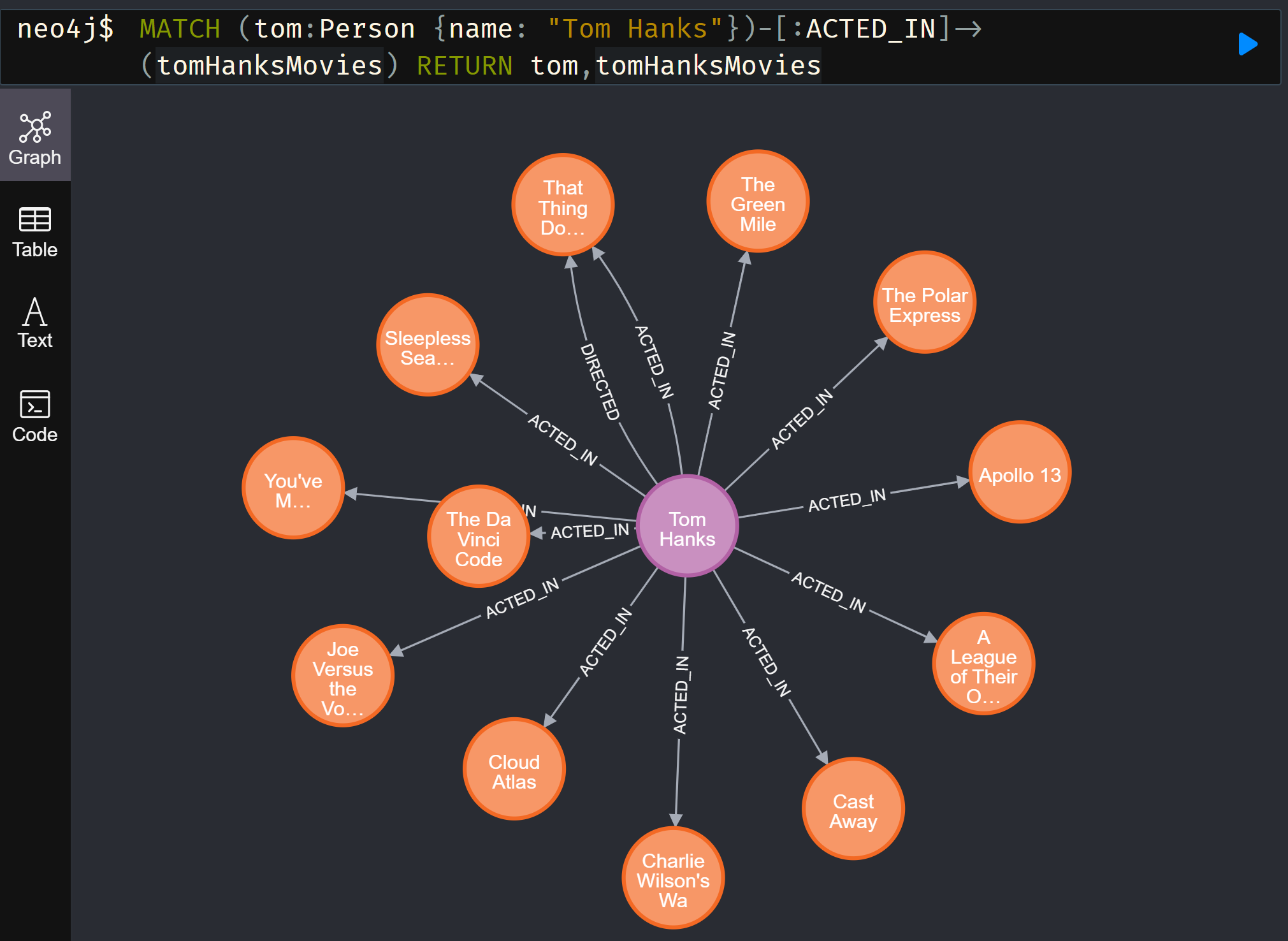
(caption: Visual search on knowledge graph using neo4j)
However, due to the large scale and automatic generation of knowledge graphs, there may be missing facts: that is, some facts may not be included in the triplets stored in the knowledge graph. These missing facts will cause the search to fail to obtain a complete answer, affecting the application of the knowledge graph. Therefore, the knowledge graph completion model attempts to learn from the existing content of the knowledge graph, so as to infer the missing facts in the knowledge graph.
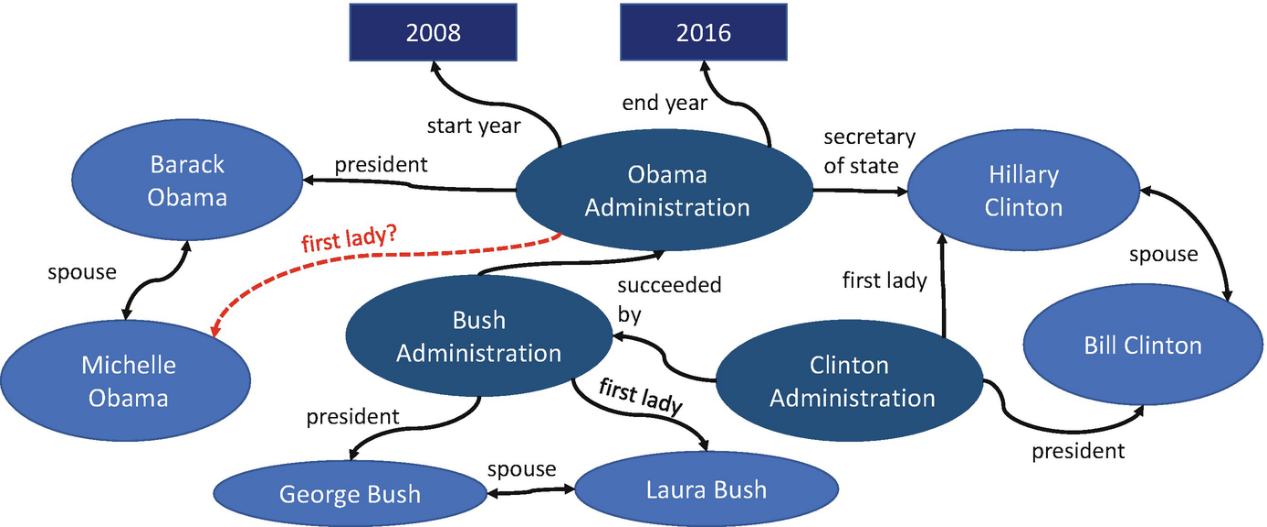
(caption: Some missing facts can be completed by reasoning from observed facts, for example: the spouse of the president is the first lady. Picture source: [[1]](https://doi.org/10.1007/978-3-030-12375-8_4))
Open-world assumption and open-world problem of knowledge graph
Notice that the knowledge graph will explicitly store the true facts and lack annotations for the false facts. Therefore, considering the situation of missing facts in the knowledge graph, for a triplet that does not appear in the storage, the user cannot judge whether it belongs to the wrong fact that should not be included, or the missing fact that has been omitted. This is called open-world assumption(OWA). The opposite of this assumption, called the closed-world assumption (CWA), assumes that the non-existent triplet must correspond to a false fact. This corresponds to a complete knowledge graph.

(caption: The difference between OWA and CWA)
When evaluating the knowledge graph completion model, since the problem is based on the incomplete knowledge graph, the OWA should be used. However, the existing evaluation process is based on the CWA, that is, for answers that are not included in the test set, they are judged as wrong answers. Therefore, there is a problem of mismatch between the actual evaluation process and the adopted assumption. This paper points out that this mismatch may lead to degradation and inconsistency of the evaluation metrics under the existing evaluation methods. The authors call it the open-world problem.
In order to study this problem, the authors model the missing facts in the test set and the correct prediction of the training model as two random events, and derive the expectation of the evaluation metric under the missing situation with the change of the model strength. Within an acceptable error range, the authors prove that for the most commonly used metric: mean reciprocal rank (MRR), its expectation presents a logarithmic curve of the model strength. This will lead to the problem of metric degradation: first, for a model that can predict correctly, the expectation of the evaluation metric cannot reach the theoretical maximum value; at the same time, the growth of the metric is too flat due to its logarithmic trend, and it cannot accurately reflect the growth of the model strength.
This degradation, coupled with the large variance shown by the numerical experiments, may lead to the problem of inconsistent metrics. That is, for models with stronger actual strength, their metrics may be worse; therefore, it will lead to the wrong comparison of the strength between models. Furthermore, if there is the correlation between the above two random events, the authors further prove the existence of model bias, that is, the metric tends to give a higher evaluation for models with negative correlation (that is, for facts missing in the test set, the model is more likely to predict incorrectly). This inconsistency of expectations cannot be solved by more test samples.
In order to verify the above theoretical results, the authors generated a family tree data set with complete facts, and then randomly deleted some facts from it to simulate the missing data set in reality. On this data set, the authors trained various knowledge graph completion models, and observed the above-mentioned metric degradation and inconsistency phenomena under different missing degrees.
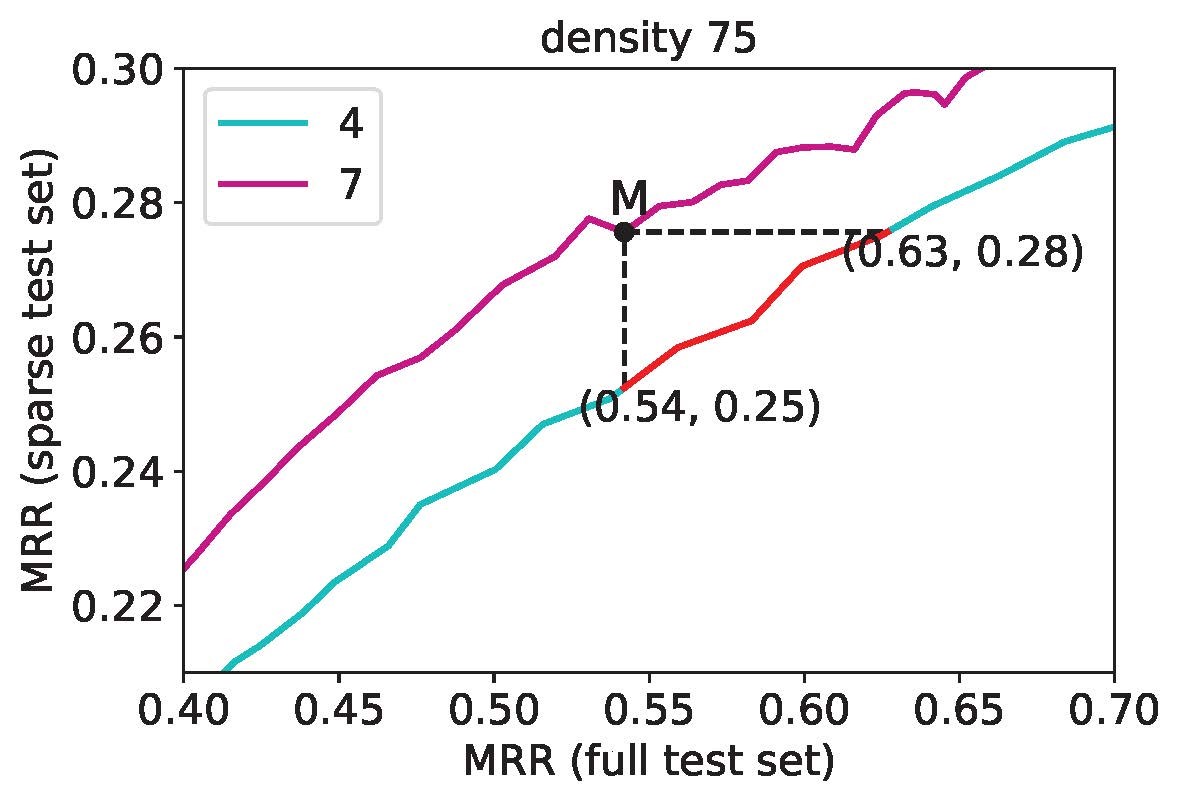
(Example: Two models as shown in the figure: the model represented by the M point and the model represented by the point on the red line segment. When the actual strength differs by 10%, the evaluation metric gives the opposite result. (The horizontal axis is the actual strength of the model, and the vertical axis is the evaluation on the missing data set.))
Finally, the authors pointed out that this phenomenon is caused by the "focus-on-top" property of metrics commonly used. It requires that the metrics is more sensitive to the change of the position of the object ranked at the top, which is to simulate the behavior of human beings paying more attention to the top position when evaluating. However, it is precisely this sensitivity that makes the metric more severely affected when facts miss. To this end, the authors proposed some metrics that pay less attention to the head, and based on theoretical and experimental verification, these metrics can indeed reduce the impact of the open-world problem on model evaluation.
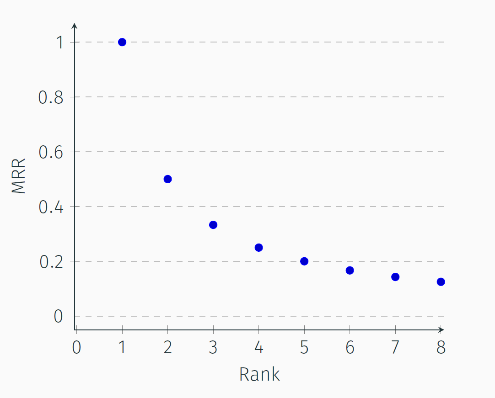
(caption: The most common metric MRR, which has an obvious "focus-on-top" property)
Summary
In this work, based on the open-world assumption of the knowledge graph, the authors theoretically deduced and experimentally verified the existence of metric degradation and inconsistency; and pointed out that the reason for this phenomenon is the "focus-on-top" property of the metric. The authors proposed to consider adding metrics that are "less focus-on-top" as the verification to avoid inaccurate and unfair comparisons. In summary, the current knowledge graph completion metrics are not perfect, and may incorrectly reflect the strength of the model. This paper points out this problem, gives theoretical and experimental verification, and proposes some solutions.


