Prof. Mu Yadong's research lab recently published a paper entitled "Neural Koopman Pooling: Control-Inspired Temporal Dynamics Encoding for Skeleton-Based Action Recognition" at the prestigious international computer vision conference CVPR 2023. The first author is Mr. Wang Xinghan, the second author is an undergraduate student Mr. Xu Xin from the Turing Class of grade 2019, and the corresponding author is Mu Yadong, an associate professor affiliated with Wangxuan Institute of Computer Technology. In this work, they proposed a pooling method for sequential data based on the Koopman operator of nonlinear control. The inability of existing pooling layers in deep neural networks to capture high-order dynamic information in sequential data prompted the authors to propose a plug-and-play parameterized pooling module based on the Koopman operator. Specifically, they linearized nonlinear systems and utilized a linear evolution matrix to represent complex systems. Furthermore, they introduced an eigenvalue regularization scheme to enforce the stability of the learned linear system. Experimental results demonstrate that this method significantly improves model performance in both fully supervised and one-shot learning settings. The code for this work is publicly available at https://github.com/Infinitywxh/Neural_Koopman_pooling.
Skeleton-based action recognition is an important task in the field of computer vision, aimed at classifying human actions using skeletal sequences. In recent years, with the rise of deep learning, many existing methods have adopted convolutional or graph neural networks to extract spatiotemporal features from skeletal sequences and used average pooling to aggregate temporal information (as shown in Figure 1). However, temporal average pooling only contains first-order information. Therefore, recent works have explored second-order pooling schemes such as bilinear pooling or covariance pooling that captures second-order information between adjacent frames or different channel features. However, skeletal sequences have complex temporal dynamics, yet existing pooling methods have not explicitly described such dynamics, resulting in inadequate temporal modeling.

Figure 1: Temporal average pooling (left) and linear dynamics based high-order pooling (right).
The core idea of this work is to utilize Koopman theory to characterize the dynamics of the sequence. Koopman theory aims to map complex nonlinear dynamic systems into linear ones, making it possible to investigate the system using mathematical tools such as spectral analysis. This method has been widely applied in time series analysis and other fields. In addition to traditional dynamic mode decomposition (DMD), recent works have combined deep learning with Koopman theory using autoencoder and specially designed loss functions to ensure the linearity of the system in an end-to-end manner. However, most existing works have focused on sequence prediction tasks and have not explored the application of the Koopman operator in sequence recognition tasks.
To address the limitations of existing pooling methods, this work uses Koopman theory to design an end-to-end trainable plug-and-play high-order pooling module, which can explicitly model the spatio-temporal interactions of features. As shown in Figure 2, compared to previous methods, this approach views the temporal evolution of the skeleton sequence as a dynamical system and uses a backbone network to embed it into some space, where the temporal dynamics is linear. The evolution matrix K in this linear space can be seen as the signature of this sequence, which contains rich high-order temporal information. For the classification task, since each category has its specific dynamical pattern, we set N learnable Koopman matrices Ki (with a size of C*C, where C represents the feature dimension, and N is the number of categories) to represent the linear evolution of each category. During classification, the result can be obtained by comparing the linear evolution matrix K of the given sequence with the evolution matrix Ki of each category.

Figure 2: Computational pipeline of Koopman-based pooling.
Compared to models such as recurrent neural networks (RNNs), Koopman theory has better theoretical interpretability, and the spectrum and eigenvalues of the linear evolution matrix K determine the dynamics of the entire system. Most of the related works on Koopman theory mainly focus on how the stability influences long-term prediction, but rare work has explored the role of stability in recognition tasks. As shown in Figure 3, 'original' refers to the trajectory of the original sequence, and the trajectory labeled 'i' is the result of 1-step evolution of features using the evolution matrix of class i. Ideally, the blue line (original trajectory) and the black line (trajectory evolved using the evolution matrix of the true class) should overlap. It can be observed that a decaying or unstable system will lead to errors in linear fitting, thereby reducing the accuracy of classification. To address this issue, we propose an eigenvalue regularization technique that pushes the eigenvalues of the linear evolution matrix K towards the unit circle, making their magnitude close to 1, thus ensuring that the learned linear system is stable and does not decay.
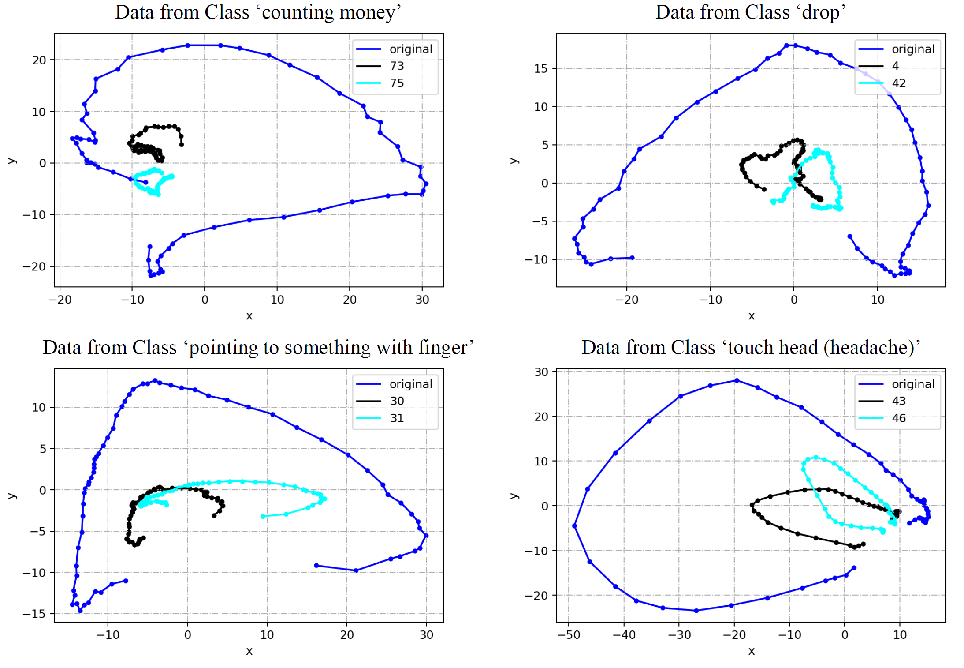
Figure 3: Decaying linear systems lead to matching and classification errors.
This method performs particularly well in one-shot learning. In one-shot learning, since only one example sample is provided for each category, it is crucial to fully utilize its temporal information for accurate classification. Existing methods mostly use temporal average pooling to aggregate features, and then use measures such as cosine distance for matching and classification. These matching techniques still rely on the first-order information of example samples and ignore the complex dynamic features of sequences. We combine the Koopman pooling method with dynamic mode decomposition (DMD) to design a one-shot classification framework based on temporal dynamic matching. Specifically, for the example sample X of test category i, we use the DMD method to calculate its linear evolution matrix Ki as the dynamic pattern template of this category. For each test sample, its classification result can be obtained by matching its linear evolution matrix K with the learned category templates K1~KN.
To verify the effectiveness of Koopman pooling, this paper conducted experiments in two settings, including full supervision and one-shot, on three skeleton action recognition benchmark datasets: NTU RGB+D, NTU RGB+D 120, and NW-UCLA. The experimental results show that after adding the Koopman pooling module, the performance of the baseline model CTR-GCN has been significantly improved on all datasets, especially in the one-shot learning setting. The proposed model's accuracy has increased by 2.5% and 6.6% on the NTU120 and NW-UCLA datasets, respectively, compared to previous works, demonstrating significant improvements. Figure 4 shows the visualization results of the Koopman pooling model after eigenvalue regularization, where PCA is used to embed the feature trajectories in the linear space into a 2D plane for visualization. It can be seen that after eigenvalue regularization, the decay problem of the system has been greatly alleviated, and the model can learn specific evolution patterns for different categories, thus achieving accurate classification.
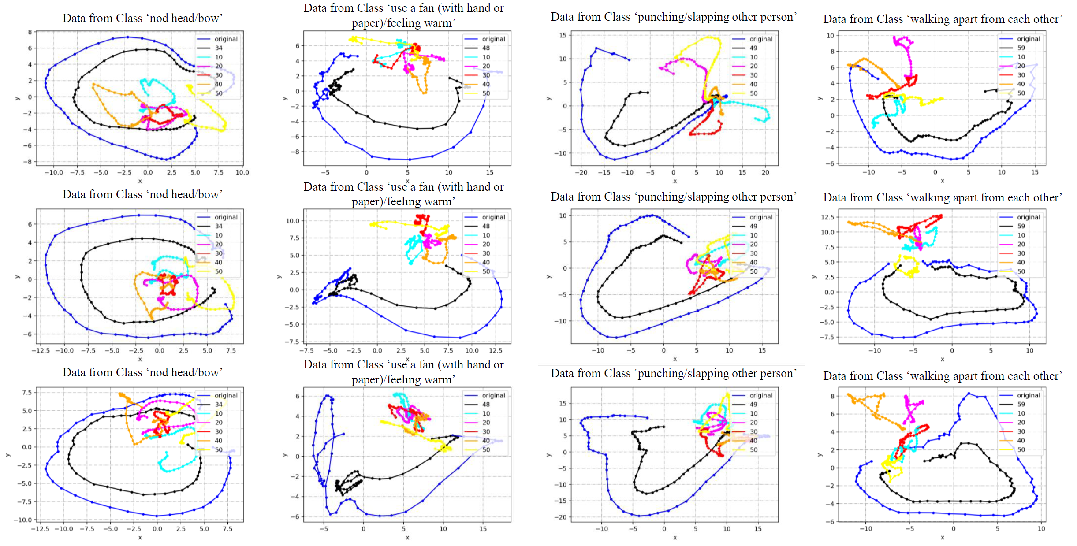
Figure 4: Visualization results of evolution trajectories in linear space.
This work demonstrates the power of combining traditional control theory with deep learning and computer vision, providing an effective approach for capturing high-order dynamic information in sequential data. This approach can be potentially extended to other computer vision and robotics tasks.


